segunda-feira, 9 de maio de 2016


 função zeta Graceli com variáveis infinitesimais progressimais.

                                                        p/pP
\zeta_K (s) = \sum_{I \subseteq O_K} (N_{K/\mathbb{Q}} (I))^{-s}   [p]
                 ____________________
                         O_K  / [p/pP]






                                          p/pP
                    ____________________
\zeta_K (s) = \sum_{I \subseteq O_K} (N_{K/\mathbb{Q}} (I))^{-s}   [p]
                 ____________________
                         O_K  / [p/pP]











                             
                              ________p/pP_____
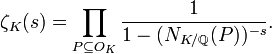\zeta_K (s) = \prod_{P \subseteq O_K} \frac{1}{1 - (N_{K/\mathbb{Q}}(P))^{-s}}. [p]
                           -_______________________
                                          O_K / I / [ p/pP]









                                                                       p/pP
                              ________p/pP_____
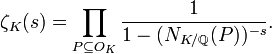\zeta_K (s) = \prod_{P \subseteq O_K} \frac{1}{1 - (N_{K/\mathbb{Q}}(P))^{-s}}. [p]
                           -_______________________
                                          O_K / I / [ p/pP]



Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)